Understanding Feed Forward Neural Networks With Maths and Statistics

From machine translation to search engines, and from mobile applications to computer assistants feed forward neural networks in deep learning is everywhere.

Machine learning algorithms and statistics algorithms can be applied to data in various ways. Deep learning models mimic the ways in which the human brain finds and creates patterns from data. Deep learning is becoming increasingly important to software engineers as it spreads throughout a variety of industries.

An artificial neural network with a circular network of nodes is called a feed forward neural network. In contrast to recurrent neural networks, feed forward neural networks cycle some routes.

The feed forward model is a basic type of neural network because the input is only processed in one direction. As part of our exploration of neural networks, we'll examine feed forward neural networks in-depth.

Why are neural networks used?

Neuronal networks can theoretically estimate any function, regardless of its complexity.

Yet, supervised learning is a method of determining the correct Y for a fresh X by learning a function that translates a given X into a specified Y. But what are the differences between neural networks and other methods of machine learning? The answer is based on the Inductive Bias phenomenon, a psychological phenomenon.

Machine learning models are built on assumptions such as the one where X and Y are related. An Inductive Bias of linear regression is the linear relationship between X and Y. In this way, a line or hyperplane gets fitted to the data.

When X and Y have a complex relationship, it can get difficult for a Linear Regression method to predict Y. For this situation, the curve must be multi-dimensional or approximate to the relationship.

A manual adjustment is needed sometimes based on the complexity of the function and the number of layers within the network. In most cases, trial and error methods combined with experience get used to accomplishing this. Hence, this is the reason these parameters are called hyperparameters.

What is a feed forward neural network?

Feed forward neural networks are artificial neural networks in which nodes do not form loops. This type of neural network is also known as a multi-layer neural network as all information is only passed forward.

During data flow, input nodes receive data, which travel through hidden layers, and exit output nodes. No links exist in the network that could get used to by sending information back from the output node.

A feed forward neural network approximates functions in the following way:

• An algorithm calculates classifiers by using the formula y = f* (x).

• Input x is therefore assigned to category y.

• According to the feed forward model, y = f (x; θ). This value determines the closest approximation of the function.

Feed forward neural networks serve as the basis for object detection in photos, as shown in the Google Photos app.

What is the working principle of a feed forward neural network?

When the feed forward neural network gets simplified, it can appear as a single layer perceptron.

This model multiplies inputs with weights as they enter the layer. Afterward, the weighted input values get added together to get the sum. As long as the sum of the values rises above a certain threshold, set at zero, the output value is usually 1, while if it falls below the threshold, it is usually -1.

As a feed forward neural network model, the single-layer perceptron often gets used for classification. Machine learning can also get integrated into single-layer perceptrons. Through training, neural networks can adjust their weights based on a property called the delta rule, which helps them compare their outputs with the intended values.

As a result of training and learning, gradient descent occurs. Similarly, multi-layered perceptrons update their weights. But, this process gets known as back-propagation. If this is the case, the network's hidden layers will get adjusted according to the output values produced by the final layer.

Layers of feed forward neural network

• Input layer:

The neurons of this layer receive input and pass it on to the other layers of the network. Feature or attribute numbers in the dataset must match the number of neurons in the input layer.

• Output layer:

According to the type of model getting built, this layer represents the forecasted feature.

• Hidden layer:

Input and output layers get separated by hidden layers. Depending on the type of model, there may be several hidden layers.

There are several neurons in hidden layers that transform the input before actually transferring it to the next layer. This network gets constantly updated with weights in order to make it easier to predict.

• Neuron weights:

Neurons get connected by a weight, which measures their strength or magnitude. Similar to linear regression coefficients, input weights can also get compared.

Weight is normally between 0 and 1, with a value between 0 and 1.

• Neurons:

Artificial neurons get used in feed forward networks, which later get adapted from biological neurons. A neural network consists of artificial neurons.

Neurons function in two ways: first, they create weighted input sums, and second, they activate the sums to make them normal.

Activation functions can either be linear or nonlinear. Neurons have weights based on their inputs. During the learning phase, the network studies these weights.

• Activation Function:

Neurons are responsible for making decisions in this area.

According to the activation function, the neurons determine whether to make a linear or nonlinear decision. Since it passes through so many layers, it prevents the cascading effect from increasing neuron outputs.

An activation function can be classified into three major categories: sigmoid, Tanh, and Rectified Linear Unit (ReLu).

• Sigmoid:

Input values between 0 and 1 get mapped to the output values.

• Tanh:

A value between -1 and 1 gets mapped to the input values.

• Rectified linear Unit:

Only positive values are allowed to flow through this function. Negative values get mapped to 0.

Function in feed forward neural network

Cost function

In a feed forward neural network, the cost function plays an important role. The categorized data points are little affected by minor adjustments to weights and biases.

Thus, a smooth cost function can get used to determine a method of adjusting weights and biases to improve performance.

Following is a definition of the mean square error cost function:

Image source

Where,

w = the weights gathered in the network

b = biases

n = number of inputs for training

a = output vectors

x = input

‖v‖ = vector v's normal length

Loss function

The loss function of a neural network gets used to determine if an adjustment needs to be made in the learning process.

Neurons in the output layer are equal to the number of classes. Showing the differences between predicted and actual probability distributions. Following is the cross-entropy loss for binary classification.

Image source

As a result of multiclass categorization, a cross-entropy loss occurs:

Image source

Gradient learning algorithm

In the gradient descent algorithm, the next point gets calculated by scaling the gradient at the current position by a learning rate. Then subtracted from the current position by the achieved value.

To decrease the function, it subtracts the value (to increase, it would add). As an example, here is how to write this procedure:

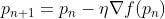
The gradient gets adjusted by the parameter η, which also determines the step size. Performance is significantly affected by the learning rate in machine learning.

Output units

In the output layer, output units are those units that provide the desired output or prediction, thereby fulfilling the task that the neural network needs to complete.

There is a close relationship between the choice of output units and the cost function. Any unit that can serve as a hidden unit can also serve as an output unit in a neural network.

Advantages of feed forward Neural Networks

• Machine learning can be boosted with feed forward neural networks' simplified architecture.

• Multi-network in the feed forward networks operate independently, with a moderated intermediary.

• Complex tasks need several neurons in the network.

• Neural networks can handle and process nonlinear data easily compared to perceptrons and sigmoid neurons, which are otherwise complex.

• A neural network deals with the complicated problem of decision boundaries.

• Depending on the data, the neural network architecture can vary. For example, convolutional neural networks (CNNs) perform exceptionally well in image processing, whereas recurrent neural networks (RNNs) perform well in text and voice processing.

• Neural networks need graphics processing units (GPUs) to handle large datasets for massive computational and hardware performance. Several GPUs get used widely in the market, including Kaggle Notebooks and Google Collab Notebooks.

Applications of feed forward neural networks

There are many applications for these neural networks. The following are a few of them.

Physiological feed forward system

It is possible to identify feed forward management in this situation because the central involuntary regulates the heartbeat before exercise.

Gene regulation and feed forward

Detecting non-temporary changes to the atmosphere is a function of this motif as a feed forward system. You can find the majority of this pattern in the illustrious networks.

Automation and machine management

Automation control using feed forward is one of the disciplines in automation.

Parallel feed forward compensation with derivative

An open-loop transfer converts non-minimum part systems into minimum part systems using this technique.

Understanding the math behind neural networks

Typical deep learning algorithms are neural networks (NNs). As a result of their unique structure, their popularity results from their 'deep' understanding of data.

Furthermore, NNs are flexible in terms of complexity and structure. Despite all the advanced stuff, they can't work without the basic elements: they may work better with the advanced stuff, but the underlying structure remains the same.

Let's begin. NNs get constructed similarly to our biological neurons, and they resemble the following:

Neurons are hexagons in this image. In neural networks, neurons get arranged into layers: input is the first layer, and output is the last with the hidden layer in the middle.

NN consists of two main elements that compute mathematical operations. Neurons calculate weighted sums using input data and synaptic weights since neural networks are just mathematical computations based on synaptic links.

The following is a simplified visualization:

In a matrix format, it looks as follows:

In the third step, a vector of ones gets multiplied by the output of our hidden layer:

Using the output value, we can calculate the result. Understanding these fundamental concepts will make building NN much easier, and you will be amazed at how quickly you can do it. Every layer's output becomes the following layer's input.

The architecture of the network

In a network, the architecture refers to the number of hidden layers and units in each layer that make up the network.

A feed forward network based on the Universal Approximation Theorem must have a "squashing" activation function at least on one hidden layer.

The network can approximate any Borel measurable function within a finite-dimensional space with at least some amount of non-zero error when there are enough hidden units.

It simply states that we can always represent any function using the multi-layer perceptron (MLP), regardless of what function we try to learn.

Thus, we now know there will always be an MLP to solve our problem, but there is no specific method for finding it.

It is impossible to say whether it will be possible to solve the given problem if we use N layers with M hidden units.

Research is still ongoing, and for now, the only way to determine this configuration is by experimenting with it.

While it is challenging to find the appropriate architecture, we need to try many configurations before finding the one that can represent the target function.

There are two possible explanations for this. Firstly, the optimization algorithm may not find the correct parameters, and secondly, the training algorithms may use the wrong function because of overfitting.

What is backpropagation in feed forward neural network?

Backpropagation is a technique based on gradient descent. Each stage of a gradient descent process involves iteratively moving a function in the opposite direction of its gradient (the slope).

The goal is to reduce the cost function given the training data while learning a neural network. Network weights and biases of all neurons in each layer determine the cost function. Backpropagation gets used to calculate the gradient of the cost function iteratively. And then update weights and biases in the opposite direction to reduce the gradient.

We must define the error of the backpropagation formula to specify i-th neuron in the l-th layer of a network for the j-th training. Example as follows (in which represents the weighted input to the neuron, and L represents the loss.)

Image source

In backpropagation formulas, the error is defined as above:

Below is the full derivation of the formulas. For each formula below, L stands for the output layer, g for the activation function, ∇ the gradient, W[l]T layer l weights transposed.

A proportional activation of neuron i at layer l based on bli bias from layer i to layer i, wlik weight from layer l to layer l-1, and akl−1 activation of neuron k at layer l-1 for training example j.

The first equation shows how to calculate the error at the output layer for sample j. Following that, we can use the second equation to calculate the error in the layer just before the output layer.

Based on the error values for the next layer, the second equation can calculate the error in any layer. Because this algorithm calculates errors backward, it is known as backpropagation.

For sample j, we calculate the gradient of the loss function by taking the third and fourth equations and dividing them by the biases and weights.

We can update biases and weights by averaging gradients of the loss function relative to biases and weights for all samples using the average gradients.

The process is known as batch gradient descent. We will have to wait a long time if we have too many samples.

If each sample has a gradient, it is possible to update the biases/weights accordingly. The process is known as stochastic gradient descent.

Even though this algorithm is faster than batch gradient descent, it does not yield a good estimate of the gradient calculated using a single sample.

It is possible to update biases and weights based on the average gradients of batches. It gets referred to as mini-batch gradient descent and gets preferred over the other two.

Ending note

The field of deep learning is one of the most studied in software engineering. Recurrent neural systems are commonly used for speech and content processing, while convolutional neural systems are best for handling images.

When processing large datasets, neural networks require massive amounts of computation power and equipment accelerators, which can be obtained by clustering graphics processing units (GPUs).

If you are new to GPUs, you can download and use free custom GPU settings on the internet. The most popular notebooks are Kaggle Notebooks and Google Collaborative Notebooks.

It can be used to solve lots of real life applications and that’s exactly why organizations have recently had huge demand for skilled professionals. However, there is an outright shortage of machine learning engineers who are adequately skilled in advanced analytics.