How to Create a Python-Based Neural Network From Scratch
•5 min read
- Languages, frameworks, tools, and trends
- Skills, interviews, and jobs
Neural networks are analogous to the human brain. This is the comparison generally made to help someone new in the field wrap their head around the concepts of machine learning and artificial neural networks. A more sophisticated approach is to define these networks as a mathematical function, simply because under the hood, it's just layers and layers of mathematical and statistical calculations.
In this article, we will build an artificial neural network from scratch using Python.
Why build a neural network from scratch with Python?
Today's programmers have numerous libraries and frameworks that make their jobs easier by providing simple and reusable functions and methods. However, having a genuine understanding of how things actually work and how a neural network operates using various mathematical equations and functions is a skill on its own.
By learning the fundamentals of creating a neural network from scratch using libraries like NumPy, Pandas, and a few others - without the help of any machine learning frameworks like TensorFlow, Keras, Sklearn, etc. - you will gain a deeper understanding and appreciation of neural networks.
Steps to build a neural network from scratch using Python
Using the Iris species dataset
For this tutorial, we will use the popular Iris species dataset that can be found on Kaggle. Our data has six columns:
- Id: Indexing
- SepalLengthCm: Length of the sepals in centimeters
- SepalWidthCm: Width of the sepals in centimeters
- PetalLengthCm: Length of the petal in centimeters
- PetalWidthCm: Width of the petals in centimeters
- Species: Species name.
Importing libraries
import numpy as np #Linear algebra and mathematical operations
import pandas as pd #importing and loading data
from sklearn.preprocessing import OneHotEncoder
Next, we’ll use Pandas to load and shuffle the dataset. A random shuffle like this helps make the data more homogenous and is a good practice to prevent overfitting in the future.
iris_df = pd.read_csv("../input/Iris.csv")
iris_df = iris_df.sample(frac=1).reset_index(drop=True) # Shuffle
Let’s see our data:
iris_df.head()
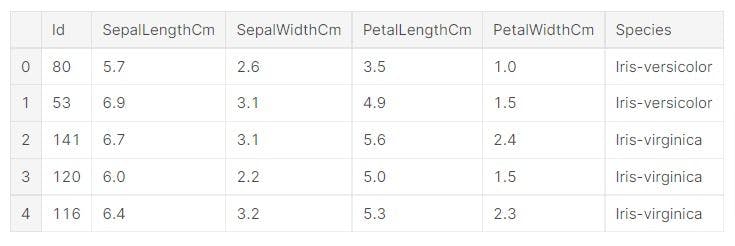
Next, we switch from pandas DataFrame to a numpy Array so that the data can be easily fed into our custom neural network.
X = iris_df[['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm']]
X = np.array(X)
X[:5]
Since the ‘Species’ column is categorical, we have to change it to one-hot encoded. As we’re still in the data preprocessing stage, it is easier to use the ‘OneHotEncoder’ from the sklearn.preprocessing library.
one_hot_encoder = OneHotEncoder(sparse=False)
Y = iris_df.Species
Y = one_hot_encoder.fit_transform(np.array(Y).reshape(-1, 1))
Y[:5]
It’s now time for the test/train/validation split. We’ll again use sklearn for this.
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.15)
X_train, X_val, Y_train, Y_val = train_test_split(X_train, Y_train, test_size=0.1)
Architecture of a deep neural network
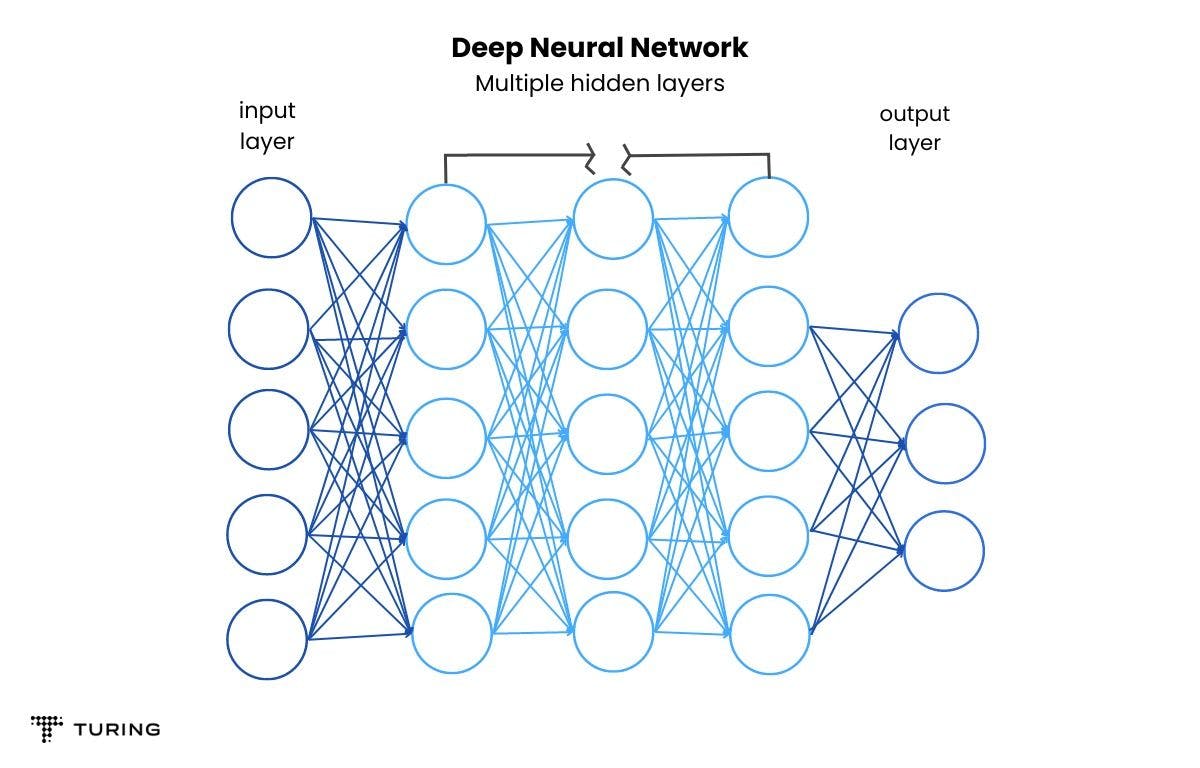
A neural network consists of:
- An input layer
- Single or multiple hidden layers
- An output layer
- Weights and biases to rank the features by importance
- An activation function, e.g., Sigmoid.
Let’s code the neural network class:
def NeuralNetwork(X_train, Y_train, X_val=None, Y_val=None, epochs=10, nodes=[], lr=0.15):
hidden_layers = len(nodes) - 1
weights = InitializeWeight(nodes)
for epoch in range(1, epochs+1):
weights = Train(X_train, Y_train, lr, weights)
if(epoch % 20 == 0):
print("Epoch {}".format(epoch))
print("Training Accuracy:{}".format(Accuracy(X_train, Y_train, weights)))
if X_val.any():
print("Validation Accuracy:{}".format(Accuracy(X_val, Y_val, weights)))
return weights
Where
- X_train, Y_train: The train set
- X_val, Y_val: Validation set (optional)
- epochs: Number of cycles (default = 10)
- nodes: An integer list of number of nodes in every layer
- lr: learning rate α (default = 0.15).
The function InitializeWeight is used to randomly initialize the weights of the nodes in the inclusive range of -1 and 1. For the implementation, we use numpy for random value generation:
def InitializeWeight(nodes):
layers, weights = len(nodes), []
for i in range(1, layers):
w = [[np.random.uniform(-1, 1) for j in range(nodes[i-1] + 1)]
for k in range(nodes[i])]
weights.append(np.matrix(w))
return weights
These weights will be later updated using the famous backpropagation algorithm. For this to work, we need forward propagation where all the inputs are multiplied and added with their respective weights and biases.
Using forward propagation
def ForwardPropagation(x, weights, layers):
activations, layer_input = [x], x
for j in range(layers):
activation = Sigmoid(np.dot(layer_input, weights[j].T))
activations.append(activation)
layer_input = np.append(1, activation)
return activations
- Every layer gets inputs from its previous layer, except the first layer of the neural network.
- The input values are then multiplied with their corresponding weights. Bias is added and passed through an activation function.
- The process is repeated across all layers. The output of the final layer is the prediction of our neural network.
Using backpropagation
Since we randomly initialize the weights at the beginning of the learning process, the output after the first run may be off course from the actual answer. The backpropagation algorithm is used to combat this by calculating the error from the final layer and updating the weights in the neural network accordingly.
Here’s the Python code:
def BackPropagation(y, activations, weights, layers):
outputFinal = activations[-1]
error = np.matrix(y - outputFinal) # Error after 1 cycle
for j in range(layers, 0, -1):
currActivation = activations[j]
if(j > 1):
# Append previous
prevActivation = np.append(1, activations[j-1])
else:
# First hidden layer
prevActivation = activations[0]
delta = np.multiply(error, SigmoidDerivative(currActivation))
weights[j-1] += lr * np.multiply(delta.T, prevActivation)
wc = np.delete(weights[j-1], [0], axis=1)
error = np.dot(delta, wc) #current layer error
return weights
All the different sections of our neural network are now built. The sample data is first sent through the network by forwarding pass. At the end of the layer, the errors are calculated and back-propagated to update the weights of the layers accordingly.
Here’s the Python implementation:
def Train(X, Y, lr, weights):
layers = len(weights)
for i in range(len(X)):
x, y = X[i], Y[i]
x = np.matrix(np.append(1, x))
activations = ForwardPropagation(x, weights, layers)
weights = BackPropagation(y, activations, weights, layers)
return weights
Using sigmoid activation function
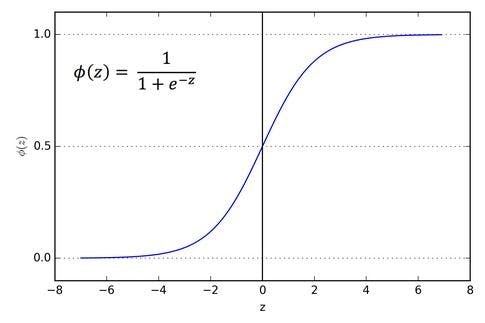
For our network, we’ll use a sigmoid activation function. The dot product of each layer is passed through an activation function which determines the final output of that layer. Sigmoid has a range of (0,1). It is mainly used in models where we require a prediction of probability (hence, the range 0 to 1). Since our model has to ‘guess’ the species of the flower, the sigmoid function is the best bet.
def Sigmoid(x):
return 1 / (1 + np.exp(-x))
def SigmoidDerivative(x):
return np.multiply(x, 1-x)
Prediction class
The final output from our network will be of the form [ i, j, k ], corresponding to the three classes where i, j, k are real numbers in the range [0,1]. The higher the value, the higher the chances of it being the correct class. Our job is to set the highest value at 1 and the rest at 0, where 1 denotes the predicted class.
Here’s the Python code :
def Predict(item, weights):
layers = len(weights)
item = np.append(1, item)
# Forward prop.
activations = ForwardPropagation(item, weights, layers)
Foutput = activations[-1].A1
index = FindMaxActivation(outputFinal)
y = [0 for j in range(len(Foutput))]
y[index] = 1
return y
def FindMaxActivation(output):
m, index = output[0], 0
for i in range(1, len(output)):
if(output[i] > m):
m, index = output[i], i
return index
Network evaluation
Finally, we evaluate the predictions of our neural network by taking in the predicted class and comparing it against the actual class to give us the accuracy in percentage.
Many types of evaluation metrics are available, but for the scope of this article, we will use a simple percentage measure.
ef Accuracy(X, Y, weights):
correct = 0
for i in range(len(X)):
x, y = X[i], list(Y[i])
guess = Predict(x, weights)
if(y == guess):
# Right prediction
correct += 1
return correct / len(X)
Deploying our neural network
Our neural network is complete! Let's run it and check the results.
f = len(X[0]) # no. of features
o = len(Y[0]) # no. of classes
layers = [f, 5, 10, o] # no. of nodes
L, E = 0.15, 100
weights = NeuralNetwork(X_train, Y_train, X_val, Y_val, epochs=E,
nodes=layers, lr=L);
Output:
Now, it’s time to find our network’s accuracy:
print("Testing Accuracy: {}".format(Accuracy(X_test, Y_test, weights)))
Thus, we have successfully created a Python-based neural network from scratch without using any of the machine learning libraries. Practice this tutorial until you get the hang of building your own neural network.
FAQs
1. Can a neural network handle categorical data?
Ans: Yes, a neural network can handle categorical variables as easily as numeric ones. The trick is to change the categorical values into numeric form like we did use one-hot encoding to represent the three iris species into three distinct classes.
2. How does a neural network predict?
Ans: A neural network leverages weights and biases along with ‘backward propagation’ of the error to learn and predict more accurate outcomes.
3. What are neural networks used for?
Ans: Neural networks are the fundamental building blocks of deep learning architectures. Some of its applications are face recognition, stock price prediction, healthcare, weather forecasting, self-driving cars, etc.