Different Types of Cross-Validations in Machine Learning and Their Explanations
•6 min read
- Languages, frameworks, tools, and trends

Machine learning and proper training go hand-in-hand. You can’t directly use or fit the model on a set of training data and say ‘Yes, this will work.’ To ensure that the model is correctly trained on the data provided without much noise, you need to use cross-validation techniques. These are statistical methods used to estimate the performance of machine learning models.
This article will introduce you to the different types of cross-validation techniques, supported with detailed explanations and code.
Types of cross-validation
- K-fold cross-validation
- Hold-out cross-validation
- Stratified k-fold cross-validation
- Leave-p-out cross-validation
- Leave-one-out cross-validation
- Monte Carlo (shuffle-split)
- Time series (rolling cross-validation)
K-fold cross-validation
In this technique, the whole dataset is partitioned in k parts of equal size and each partition is called a fold. It’s known as k-fold since there are k parts where k can be any integer - 3,4,5, etc.
One fold is used for validation and other K-1 folds are used for training the model. To use every fold as a validation set and other left-outs as a training set, this technique is repeated k times until each fold is used once.
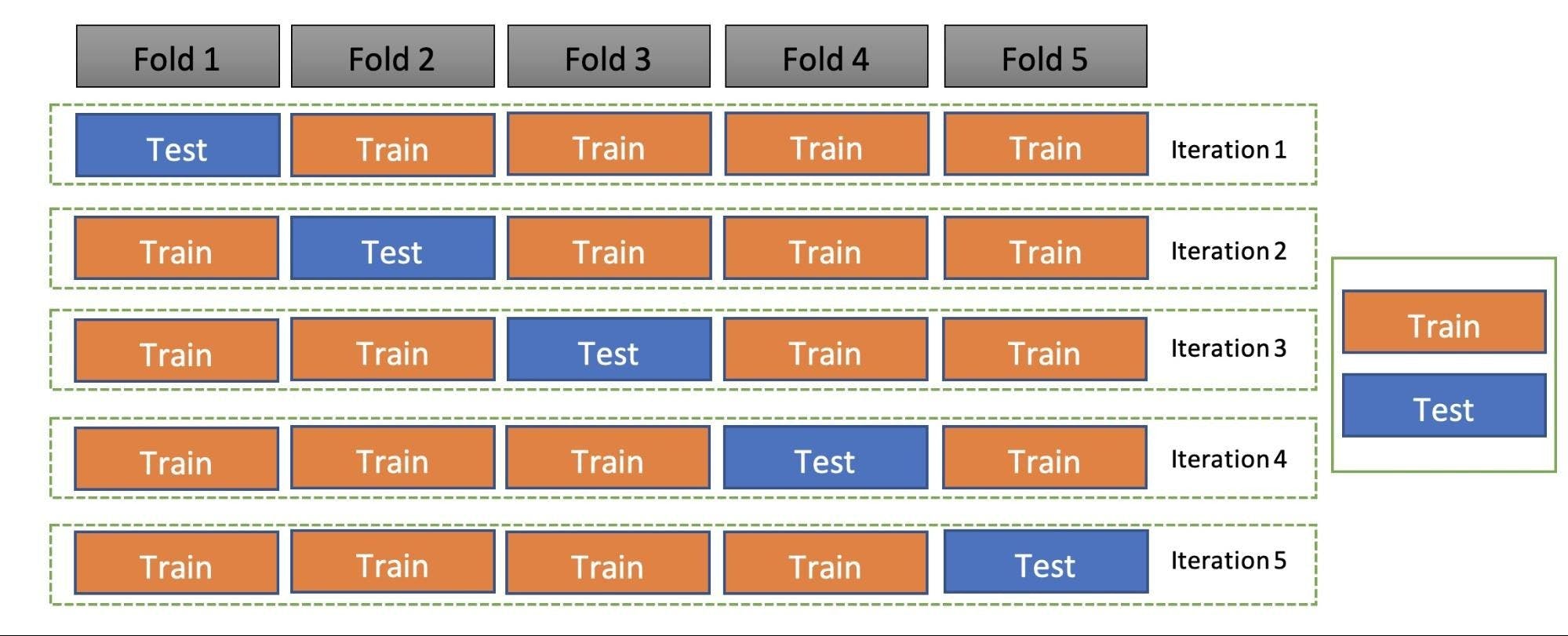
Image source: sqlrelease.com
The image above shows 5 folds and hence, 5 iterations. In each iteration, one fold is the test set/validation set and the other k-1 sets (4 sets) are the train set. To get the final accuracy, you need to take the accuracy of the k-models validation data.
This validation technique is not considered suitable for imbalanced datasets as the model will not get trained properly owing to the proper ratio of each class's data.
Here’s an example of how to perform nok-fold cross-validation using Python.
Code:
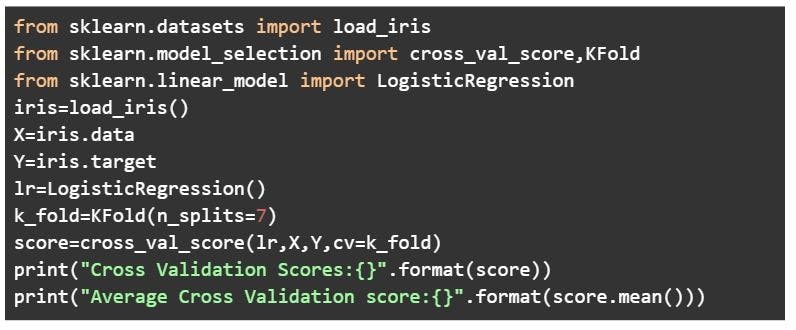
Image source: Author
Output:

Holdout cross-validation
Also called a train-test split, holdout cross-validation has the entire dataset partitioned randomly into a training set and a validation set. A rule of thumb to partition data is that nearly 70% of the whole dataset will be used as a training set and the remaining 30% will be used as a validation set. Since the dataset is split into only two sets, the model is built just one time on the training set and executed faster.
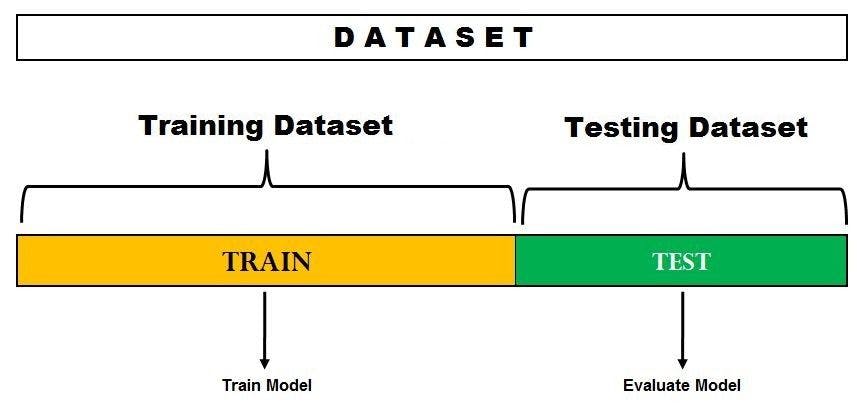
Image source: datavedas.com
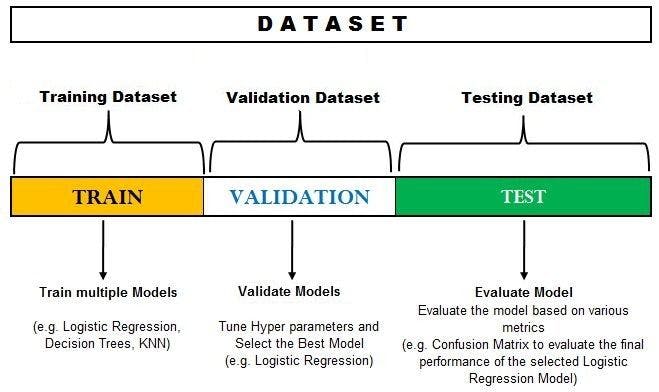
In the image above, the dataset is split into a training set and a test set. You can train the model on the training set and test it on the testing dataset. However, if you want to hyper-tune your parameters or want to select the best model, you can make a validation set like the one below.
Code:
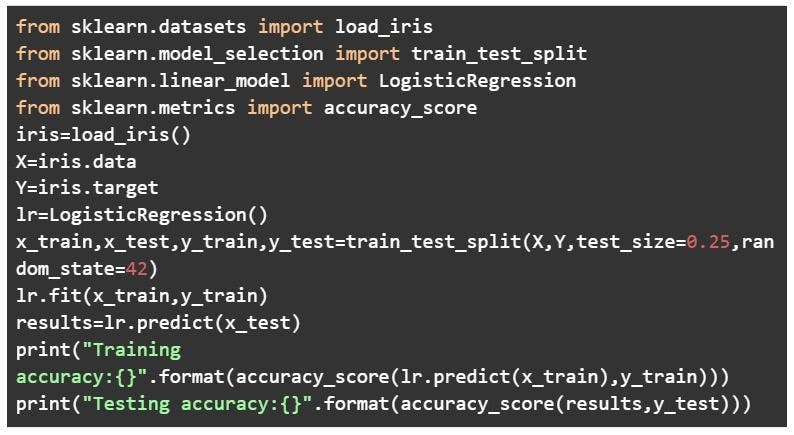
Output:

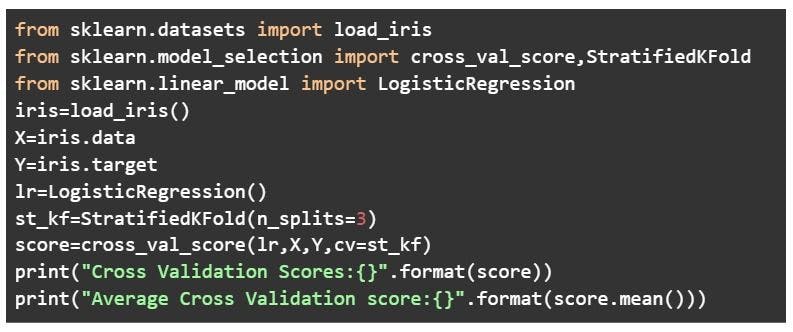
Stratified k-fold cross-validation
As seen above, k-fold validation can’t be used for imbalanced datasets because data is split into k-folds with a uniform probability distribution. Not so with stratified k-fold, which is an enhanced version of the k-fold cross-validation technique. Although it too splits the dataset into k equal folds, each fold has the same ratio of instances of target variables that are in the complete dataset. This enables it to work perfectly for imbalanced datasets, but not for time-series data.
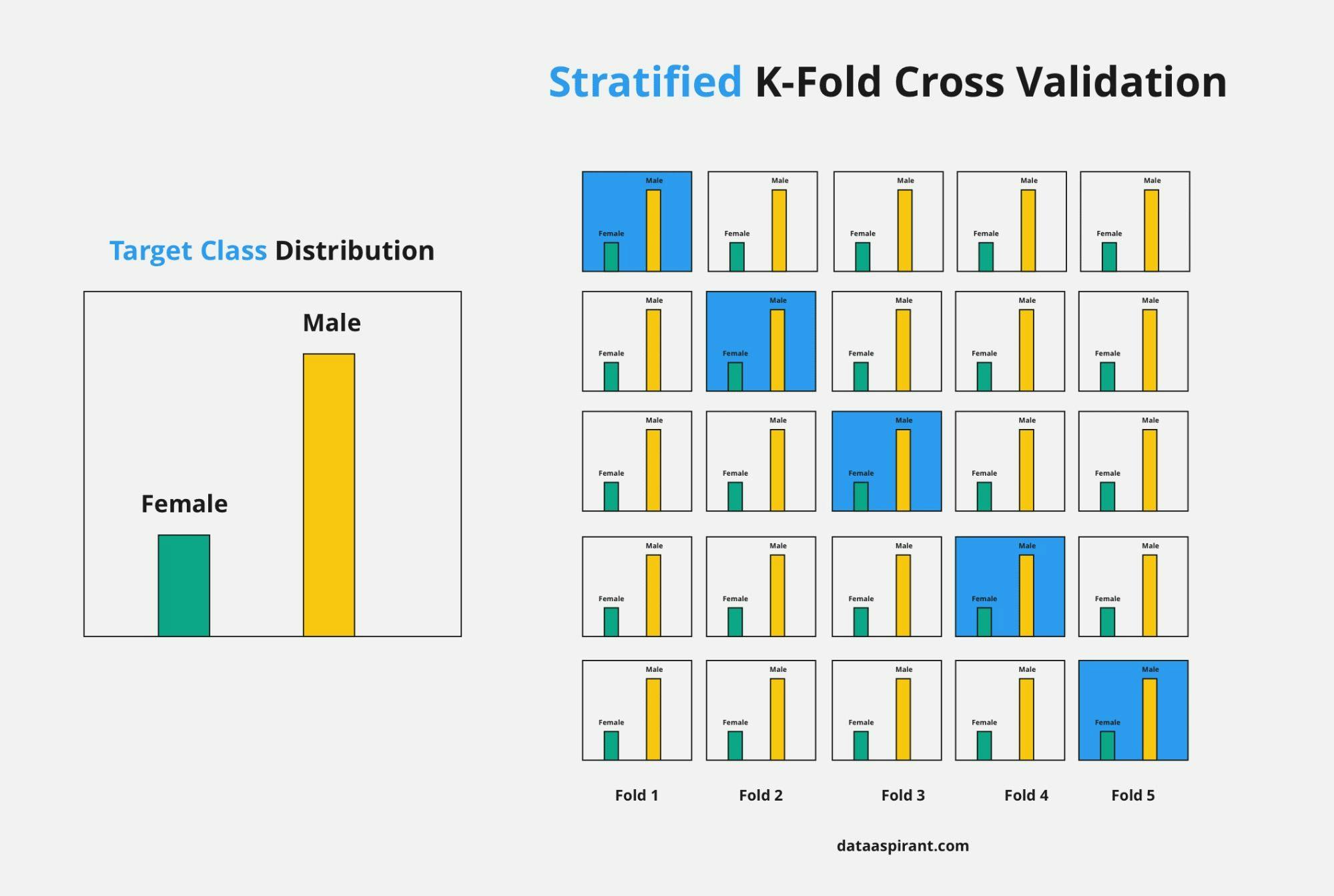
Image source: dataaspirant.com
In the example above, the original dataset contains females that are a lot less than males, so this target variable distribution is imbalanced. In the stratified k-fold cross-validation technique, this ratio of instances of the target variable is maintained in all the folds.

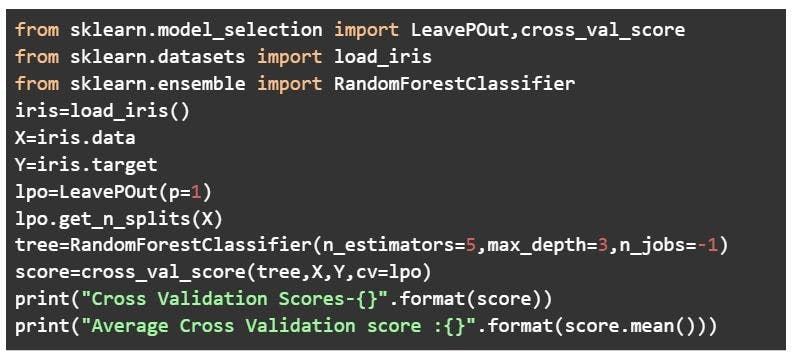
Leave-p-out cross-validation
An exhaustive cross-validation technique, p samples are used as the validation set and n-p samples are used as the training set if a dataset has n samples. The process is repeated until the entire dataset containing n samples gets divided on the validation set of p samples and the training set of n-p samples. This continues till all samples are used as a validation set.
The technique, which has a high computation time, produces good results. However, it’s not considered ideal for an imbalanced dataset and is deemed to be a computationally unfeasible method. This is because if the training set has all samples of one class, the model will not be able to properly generalize and will become biased to either of the classes.
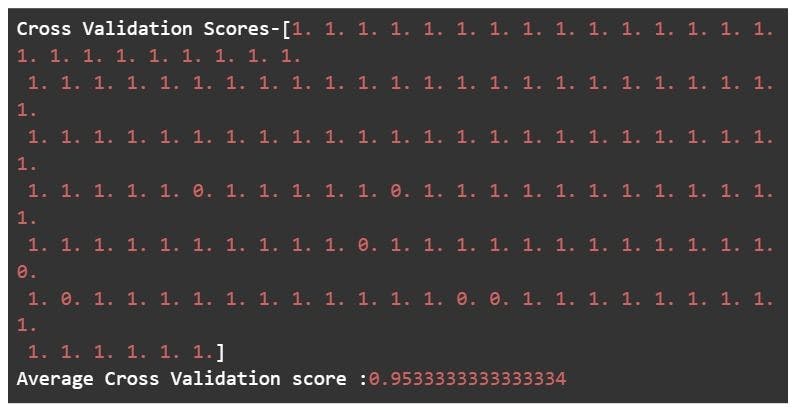
Leave-one-out cross-validation
In this technique, only 1 sample point is used as a validation set and the remaining n-1 samples are used in the training set. Think of it as a more specific case of the leave-p-out cross-validation technique with P=1.
To understand this better, consider this example:
There are 1000 instances in your dataset. In each iteration, 1 instance will be used for the validation set and the remaining 999 instances will be used as the training set. The process repeats itself until every instance from the dataset is used as a validation sample.
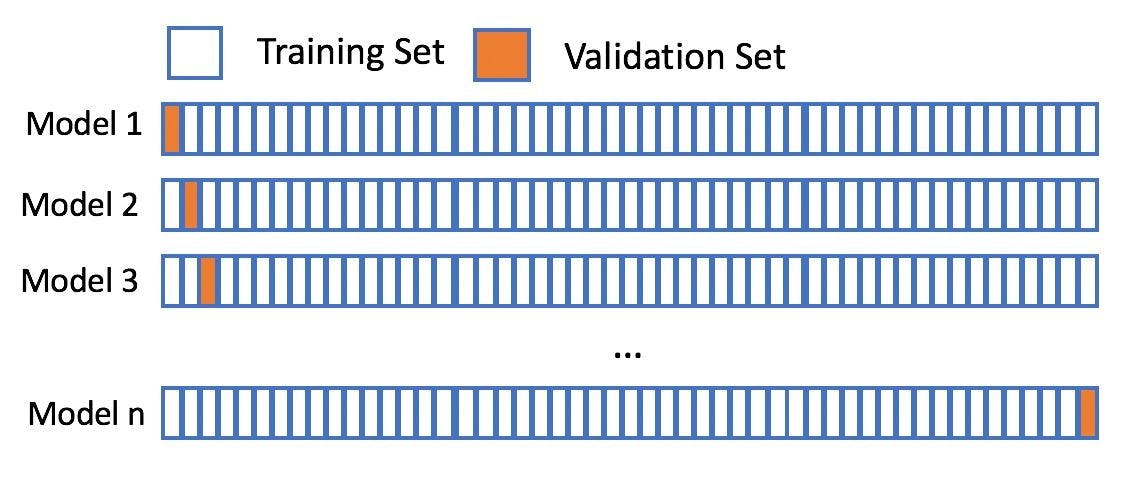
Image source
The leave-one-out cross-validation method is computationally expensive to perform and shouldn’t be used with very large datasets. The good news is that the technique is very simple and requires no configuration to specify. It also provides a reliable and unbiased estimate for your model performance.
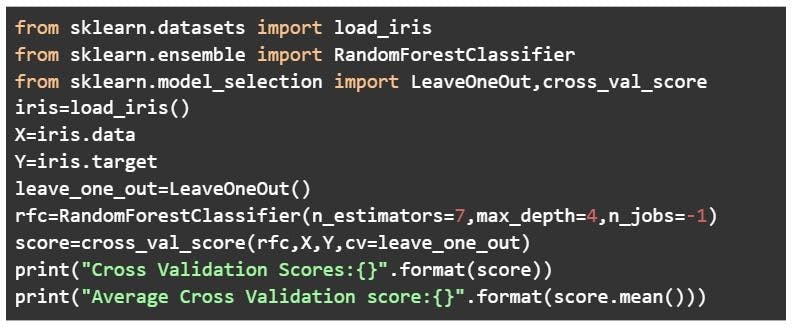
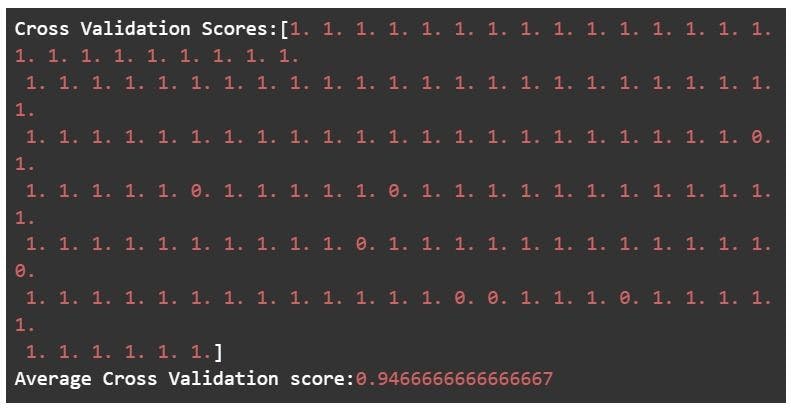
Monte Carlo cross-validation
Also known as shuffle split cross-validation and repeated random subsampling cross-validation, the Monte Carlo technique involves splitting the whole data into training data and test data. Splitting can be done in the percentage of 70-30% or 60-40% - or anything you prefer. The only condition for each iteration is to keep the train-test split percentage different.
The next step is to fit the model on the train data set in that iteration and calculate the accuracy of the fitted model on the test dataset. Repeat these iterations many times - 100,400,500 or even higher - and take the average of all the test errors to conclude how well your model performs.
For a 100-iteration run, the model training will look like this:
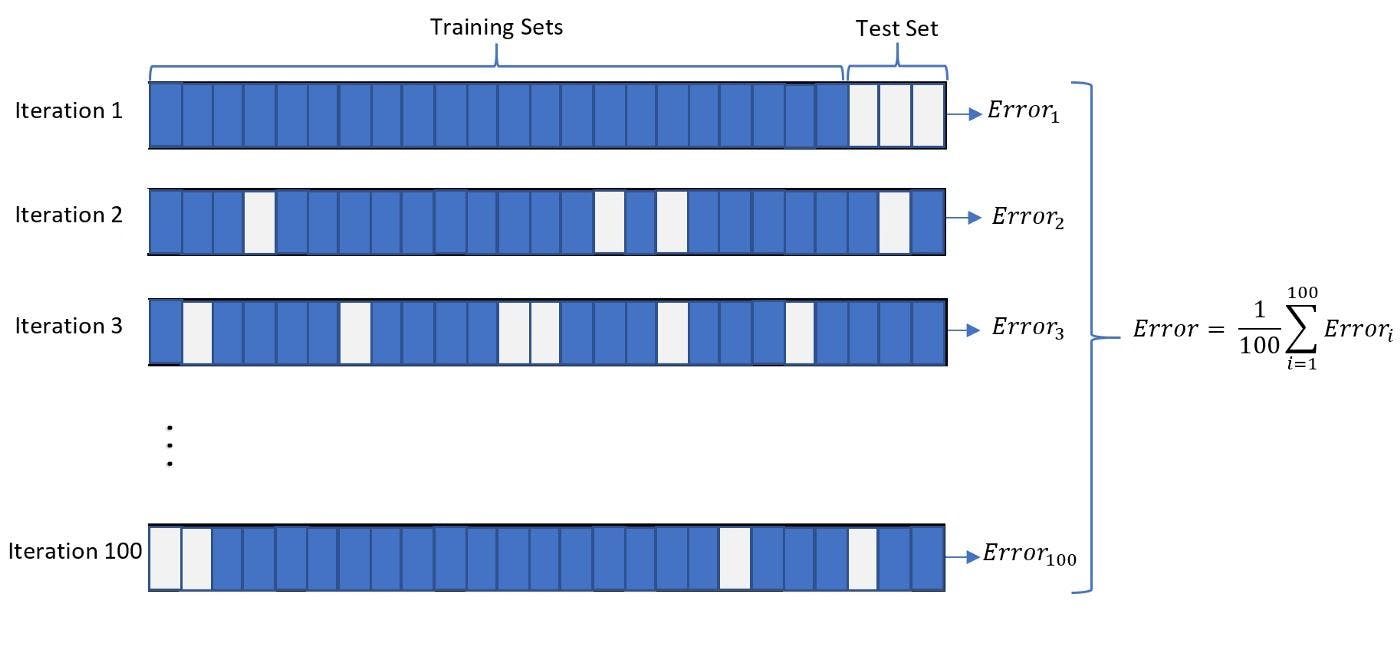
Image source: medium.com
You can see that in each iteration, the split ratio of the training set and test set is different. The average has been taken to get the test errors.
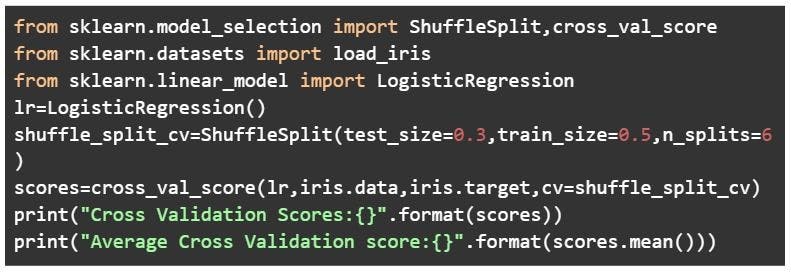

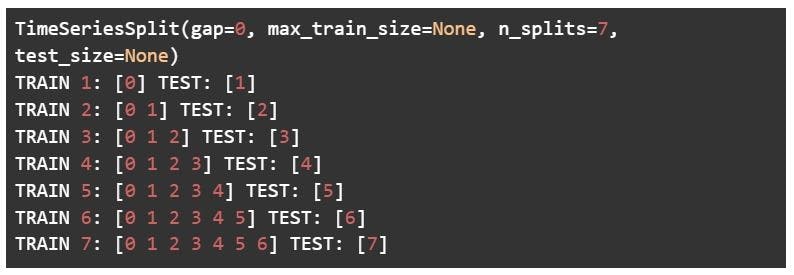
Time series (rolling cross-validation / forward chaining method)
Before going into the details of the rolling cross-validation technique, it’s important to understand what time-series data is.
Time series is the type of data collected at different points in time. This kind of data allows one to understand what factors influence certain variables from period to period. Some examples of time series data are weather records, economic indicators, etc.
In the case of time series datasets, the cross-validation is not that trivial. You can’t choose data instances randomly and assign them the test set or the train set. Hence, this technique is used to perform cross-validation on time series data with time as the important factor.
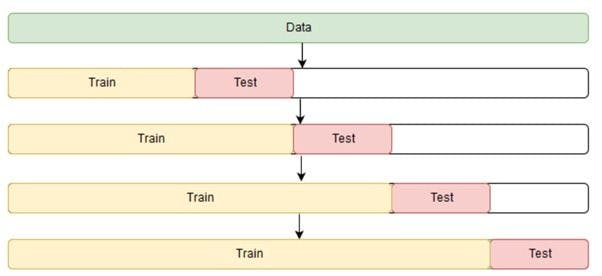
Since the order of data is very important for time series-related problems, the dataset is split into training and validation sets according to time. Therefore, it’s also called the forward chaining method or rolling cross-validation.
To begin:
Start the training with a small subset of data. Perform forecasting for the later data points and check their accuracy. The forecasted data points are then included as part of the next training dataset and the next data points are forecasted. The process goes on.
The image below shows the method.
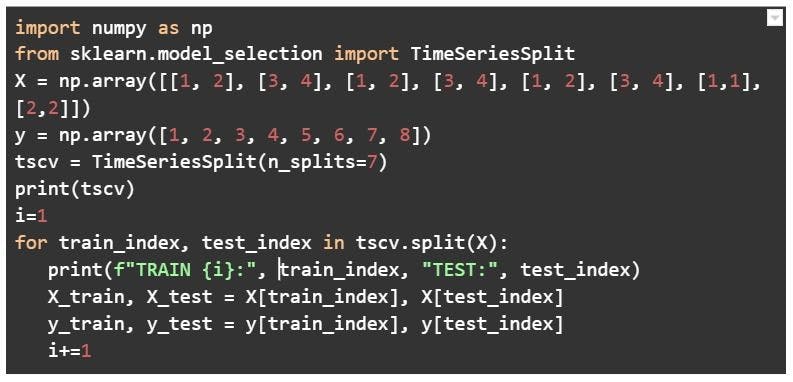
Try your hand at these codes and play around with them to get a hang of how cross-validation is done using these seven techniques.
Happy coding!