Theory of Computation With Finite State Machines

Automata theory or the theory of computation is a theoretical division of mathematics and computer science. It deals with the logic of computation concerning simple machines. An automata theory is a finite state machine, which is best known as finite automation. Automata enable scientists in understanding how machines compute functions and solve problems.

The major motivation behind the development of the theory of computation is to develop methods for describing and analyzing the dynamic behavior of discrete systems. Automata first originated from the word Automaton which is related to Automation. Symbols (characters), strings, and alphabets are the fundamental terminologies that can be understood from the theory of computation. Let’s get into finite state machines in detail.

What is a finite state machine?

A finite state machine is a conceptual tool for designing systems. It will process a sequence of inputs that will change the state of the system. When you process all the inputs, you must observe the last state of determination of the system. And also verify whether the input sequence was acceptable or not.

Finite-state automaton (FSA), finite state machine (FSM), or just a state machine is a mathematical computation model. It is an abstract machine that can be in one of a finite number of states at any given time.

The FSM might change from one state to another depending on the inputs. The change from one state to another is known as transition. An FSM can be defined by its states, the inputs, and its initial state that triggers each transition.

The finite state machines are of two different types - deterministic and non-deterministic finite state machines. A deterministic finite state machine will be equally constructed to any non-deterministic one.

You can observe the behavior of the state machines in many devices in modern society which will perform a predetermined action sequence that depends on the sequence of events that are present.

The finite state machine examples can be vending machines that dispense products when the proper coin combinations are deposited, traffic lights that can change the sequence of cars waiting, moving, and stopping can be determined, and elevators whose sequence will determine stops where to stop as per the passengers’ request.

The finite state machine has less computational power than some other computation models like the Turing machine. The computational power distinction will mean there are computational tasks that a Turing machine may do but the FSM can’t because its memory is limited by the number of states it has.

Components of the finite state machine

Below are the components which are incorporated into the finite state machine:

Initial state

The initial state is the starting point of our system. It is usually drawn with an arrow pointing to them.

Alphabet

The alphabet is also known as the language which is a set of all the valid inputs we provide.

Set of known states

A set of known states denotes that there should be a finite amount of states in our systems. But only one state will be active at a specified time. It is represented by circles.

Set of accepting states

A set of accepting states is a subset of known states. It indicates whether the input we have processed is valid or not. Accepting states can be represented with a double circle.

Transitions

The transitions are rules which will dictate how the machine moves from one state to other. It is usually represented by two states connected by a line.

Demonstration of the binary parser

Let us create a finite state machine that parses a binary sequence where each time we get a 1, we will immediately get a 0 at the same point. For example, 1010 is a valid input but it is not the case for 1101010 or 1011001. The finite state machine will be like the below:

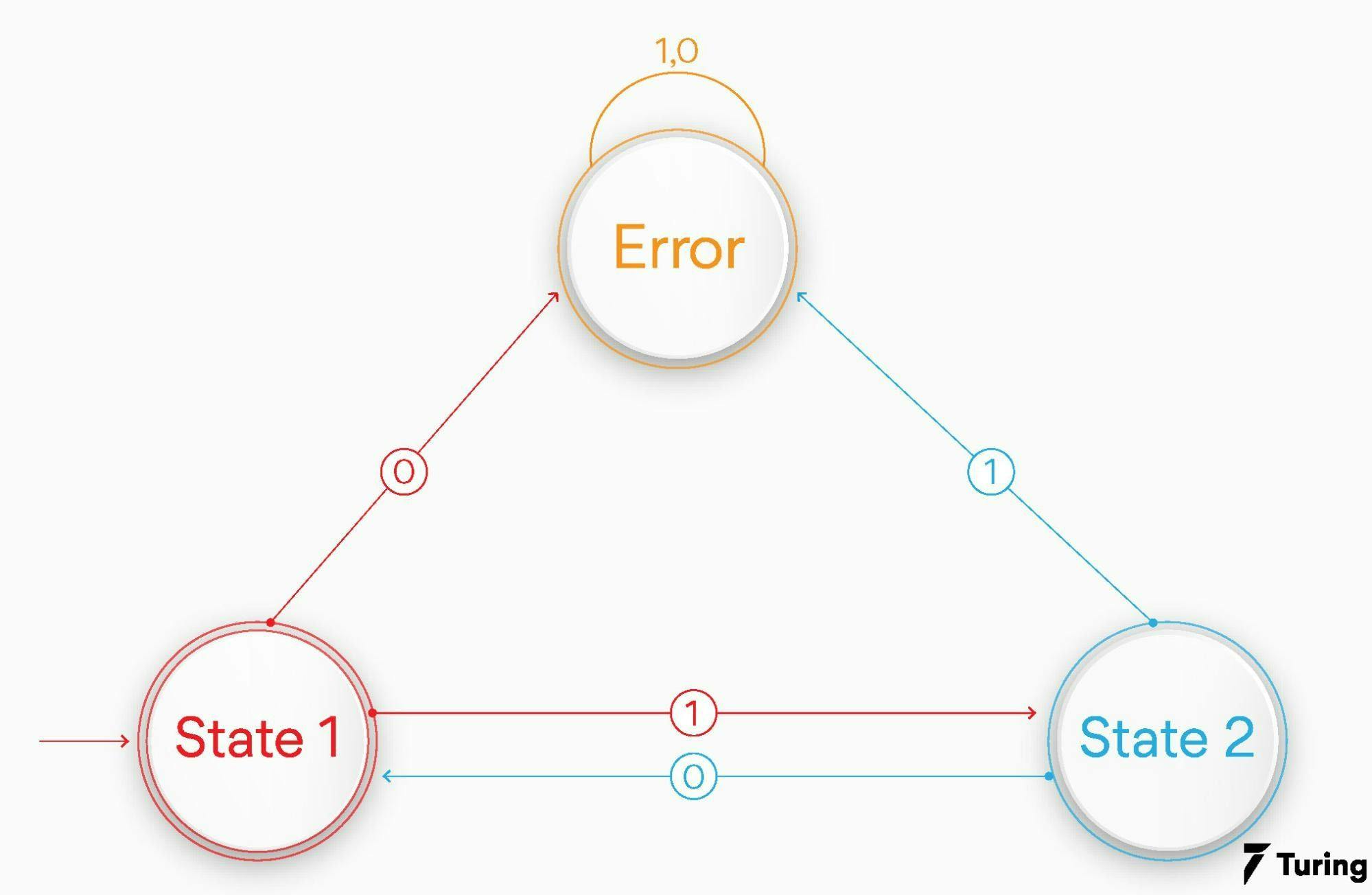
Our finite state machine has three states, state 1, state 2, and error. Here are a few possible situations:

• When you are at state 1 and get 1 as result, then you move to state 2.
• When you are at state 2 and get 0 as result, then you move back to state 1.
• When we are at state 1 and get 0 as result, then you go to the error state.
• When we are at state 2 and get 1 as result, then you also go to the error state.

As you can see, any input in the error state will stop the process as there will not be any transition out of the error state.

Creating a finite state machine in Python:

Many software implement FSM for managing some aspects of states. We can implement a finite state machine in Python and use codes to verify the inputs for a set of transitions and states.

class Transition:

	“ “ “ A change from one state to another” “ “

	def_init_(self, current_state, state_input, next_state):
		self.current_state = current_state
		self.state_input = state_input
		self.next_state = next_state

	def match(self, current_state, state_input, next_state):
	“ “ “ Determining when the state and the input satisfies this transition relation” “ “
		return self.current_state == current_state and self.state_input == state_input

	class FSM:

“ “ “A basic model for computation” “ “ 

	def_init(self, states =[ ], alphabets =[ ], accepting_states =[], initial_state = ‘ ‘):
		self.states = states
		self.alphabet = alphabet
		self.accepting_states = accepting_states
		self.inital_state = initial_state
		self.valid_transitions = False

	def add_transitions(self, transitions =[ [):
	“ “ “Before using a list of transitions, and verifying they only apply to our states” “ “
		for transition in transitions:
		if transition.current_state not in self.states:
		print(‘Invalid transition. { } is not a valid state’.format (transition.current_state))
			return 
		if transition.next_state not in self.states:
		print(‘Invalid transition. { } is not a valid state.’.format)
			return
		self.transitions = transitions
		self.valid_transitions = True
	def_accept(self, current_state,state_input):
	“ “ “Looks to see when the input for the given state matches a transition rule” “ “ 
	# If the input is valid in our alphabet
		if state_input in self.alphabet:
			for rule in self.transitions:
			if rule.match(current_state, state_input):
				return rule.next_state
			print(‘No transition for state and input’)
				return None
			return None

	def accepts(self, sequence):
	“ “ “Process an input stream for determining if the FSM will accept it” “ “
	# Check if we have transitions
		if not self.valid_transitions:
			print(‘Cannot process sequence without valid transitions’)

		print(‘Starting at { }’.format(self.initial_state))
		# When an empty sequence provided, we simply check if the initial state
		# is an accepted one 
		if len(sequence) == 0:
			return self.initial_state in self.accepting_states

	# Let’s process the initial state
	current_state = self._accept(self.initial_state, sequence[0])
		if current_state is None:
                      return False
# Continue with the rest of the sequence
for state_input in sequence[1:]:
            print(‘Current state is { }’.format(current_state))
            current_state = self._accept(current_state, state_input)
                        if current_state is None:
                                        return False
print(‘Ending state is { }’.format(current_state))
# Check if the state we have transitioned to is an accepted state
                                return current_state in self,accepting_states

Code source

The transition class will contain a match() function. When you want to know if the current state and input of the finite state machine will allow you to go to the next state-defined using the Transition class and match() function. After initializing, the FSM class will have to call the add_transitions() method.

With this method, you can validate that the transition rules are set up with valid states. Now, you can use the accepts() method with the list of inputs for determining if your machine will be accepted. Now, run a test with the binary parser which you have previously created with the below code:

# Set up our FSM with the required information:
# Set of states
states = [‘State 1’, ‘State 2’, ‘Error’]
# Set of allowed inputs
alphabet = [1, 0]
# Set of accepted states
accepting_states = [State 1’]
# The initial state
initial_state = ‘State 1’
fsm = FSM(states, alphabets, accepting_states, inital_state)

# Create the set of transitions
transition1 = Transition(‘State 1’,1, ‘State 2’)
transition2 = Transition(‘State 2’, 0, ‘State 1’)
transition3 = Transition(‘State 1’, 0, ‘Error’)
transition4 = Transition(‘State 2’, 1, ‘Error’)
transition5 = Transition(‘Error’, 1, ‘Error’)
transition6 = Transition(‘Error’, 0, ‘Error’)
transitions = [
	transition1, 
	transition2,
	transition3,
	transition4, 
	transition5,
	transition6]
# Verify and add them to the Finite State Machine
fsm.add_transitions(transitions)

# Now that our FSM is correctly set up, we can provide input for processing
# Let us transition the FSM to a green light
should_be_accepted = fsm.accepts([1, 0, 1, 0])
print(should_be_accepted)

should_be_rejected_1 = fsm.accepts([1,1,1, 0])
print(should_be_rejected_1)

# Let us transition to yellow and provide a bad input
should_be_rejected_2 = fsm.accepts([1, 0, 1, 0, 1, 0, 0])
print(should_be_rejected_2)

Code source

Finite state machine examples

FSMs are commonly used in real-world systems which extend beyond string parsing, and even software systems. Below are some examples that will provide you with a logical explanation of the working of the same.

1. Traffic lights

We can take the most simple example of a traffic light system using FSM. Let us look at each core component and identity what it means:

States: A traffic light has three stages - Green, Yellow, and Red.

Initial State: Green.

Accepting States: The traffic light runs indefinitely, so there won’t be any accepting states for this model.

Alphabet: The positive integers which represent seconds.

Transitions:

• When the traffic light is Green wait for six minutes, then go to state Yellow.
• When Yellow, wait for ten seconds, then go to state Red.
• When Red, wait for 120 seconds, then we can go to state Green.

2. Enemy artificial intelligence

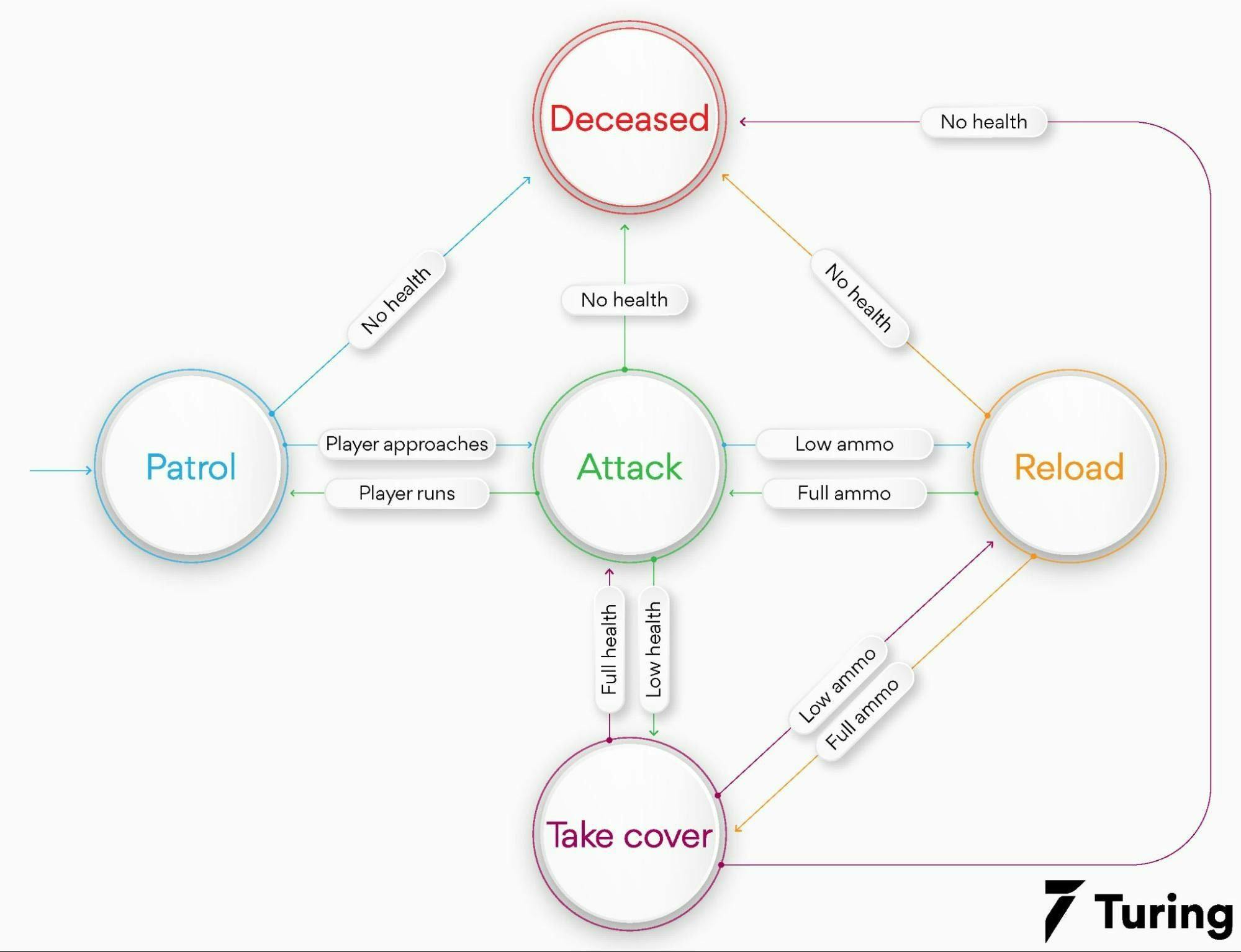
Another example is Enemy AI. FSM will allow us in mapping the flow of actions in a game’s computer-controlled players. We can take an example of an action game where the guard parols an area of the map. We can have an FSM with the below components:

States: The shooters can Patrol, Reload, Attack, Deceased, or Take Cover.

Initial state: As it is a guard, the initial state would be Patrol.

Accepting states: An enemy bot will no longer accept input when it is Deceased, so our Deceased state will be our accepting state.

Alphabet: We can use a string constant for representing a world state like Full Ammo, Low Ammo, Full Health, Player Approaches, Low Health, Player Runs, and No Health.

Transitions:
It is a tad complex model when compared to a traffic light, so we will have separate transitions for each state at a time:

- Patrol

• When a player approaches, go to the state Attach
• When we run out of health, then go to the state Deceased

- Reload

• When ammo is full, then go to the state Attack
• When health is low, then go to the state Take Cover
• When you run out of health, go to the state Deceased

- Attack

• When ammo is low, go to the state Reload
• When health is low, go to the state Take Cover
• When the player escapes, go to the State Patrol
• When you run out of health, then go to the state Deceased

- Take Cover

• When health is full, go to the state Attack
• When ammo is low, go to the state Reload
• When you run out of health, then go to the state Deceased

The FSM representation of the same is as follows:

Drawbacks

The major benefit of FSM is its simplicity, but it also becomes one of its disadvantages. Systems that need an indeterminate number of states can’t be modeled by FSM. Earlier the FSM which accepts the string ‘10’ for any number of iterations was allowed.

When we have to accept a string of any number of 1s followed by the same number of 0s, we might not be able to create an FSM. An FSM will not keep track of the number of states you have visited, it is only aware of your current state.

With the Pumping Lemma, we can now understand all the essential properties of any programming language. But rather than a classification of languages being there, no FSM can be built.

The finite state machine is a theoretical framework we can use for modeling systems. When you have a known set of states, the accepting state, the starting state, and the rules for the transitions between states, you can easily determine if a sequence of inputs can be accepted.

The limited number of states which can be modeled doesn’t make these abstract machines suitable for all systems, as in the Pumping Lemma. So, finite state machines can be used in many real-world applications and it is already quite popular.

FAQs:

1. What is a finite state machine in the theory of computation?

A mathematical model of computation is known as a finite-state automaton or finite-state machine. FSM is an abstract model which can be one of the many number of finite states at a preferred time. FSMs are a class of automata studies in the theory of automata and theory of computation.

2. What is the application of TOC?

Here is some application of TOC:

- Complexities in Natural Selection in Biology

- Deterministic Finite Automata for Compiler Design

- Models to find the limitation of Computing machines like the Halting problem

- Game of Life

- Modeling the entire universe

- Real-life computing machines and problems

- Super recursive algorithms

- Turing machine-designed algorithms

- Real-life applications like

• Video games
• Traffic lights
• Vending machines
• Speech recognition
• CPU controllers
• Natural language processing

3. Why are finite machines called so?

A finite state machine is a state machine that is a model of computation. A description of a system that waits for the execution of a transition is known as a state. The execution of a set of actions for fulfilling an event is known as transitions. It is known as finite because the machine will transition from one state to another for performing different actions, but the only state can be active at a given time.