Mathematical Optimization vs Machine Learning: A Brief Comparison

Mathematical optimization and machine learning (ML) are sophisticated technologies that are used to analyze and draw meaningful inferences from data. A beginner or novice, who’s not familiar with the literature in analytics, most likely knows of machine learning as it’s a more widely-used and popular technology. On the other hand, mathematical optimization is more of a branch of applied mathematics and is generally sought-after by mathematically-gifted and mathematically-inclined individuals.

Both technologies require a fair bit of mathematical knowledge. There’s some overlap that you’ll notice as well when you start studying them in-depth. The mathematics that’s generally advised for starting both are linear algebra (vector, matrices, etc.), graph theory, multivariate calculus (slope, gradient calculation, etc), and some basic statistics for PCA (principal component analysis). Proficiency in programming languages like Python, R, Octave, and Julia also helps.

At first glance, mathematical optimization and machine learning appear similar. Indeed, they have a lot in common, but a closer inspection of their features and practical use cases will yield some fundamental differences.

You can get a better idea by looking at their applications.

- Mathematical optimization: Electricity distribution, finance, GPS systems, logistics, manufacturing, sports scheduling, etc.
- Machine learning: Sales planning, product analysis, market research, fraud prevention, ads personalization, etc.

To understand the similarities and differences in more depth, let’s take a look at the fields themselves.

Mathematical Optimization

Linear programming led to the creation of optimization back in 1946-1947. Essentially, mathematical optimization is choosing inputs from a set of available options to get the best possible output for a given problem. It is a much more robust technique for prescriptive analysis and is used to make fast decisions to solve complex business problems.

Components of Mathematical Optimization

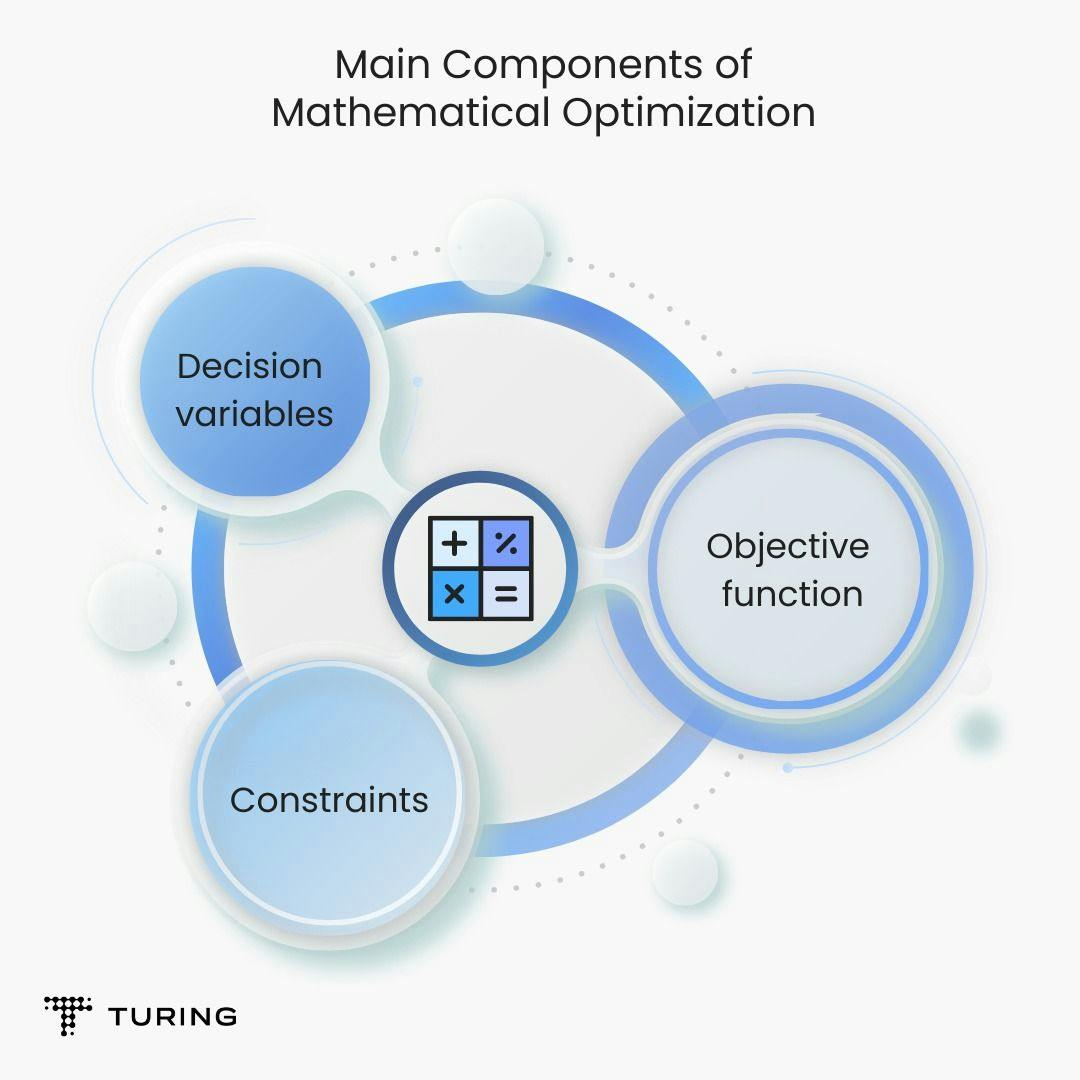
1. Decision variables: These are the input variables that a user chooses and are represented by mathematical symbols. The control variable is chosen from a series of values.

2. Objective function: This is equivalent to a machine learning model. The function takes the decision variables as inputs and maximizes or minimizes them according to business requirements. It then gives a numerical evaluation of the problem.

3. Constraints: As the name suggests, these are logical conditions that the objective function has to satisfy. They can be any physical or theoretical values that impose restrictions on decision variables.

Machine Learning

Machine learning, commonly abbreviated as ML, is a subset of artificial intelligence (AI). It helps computers mimic the human brain to a degree by gradually improving their decision-making abilities using data and algorithms.

Image source: What is reinforcement learning? | MathWorks

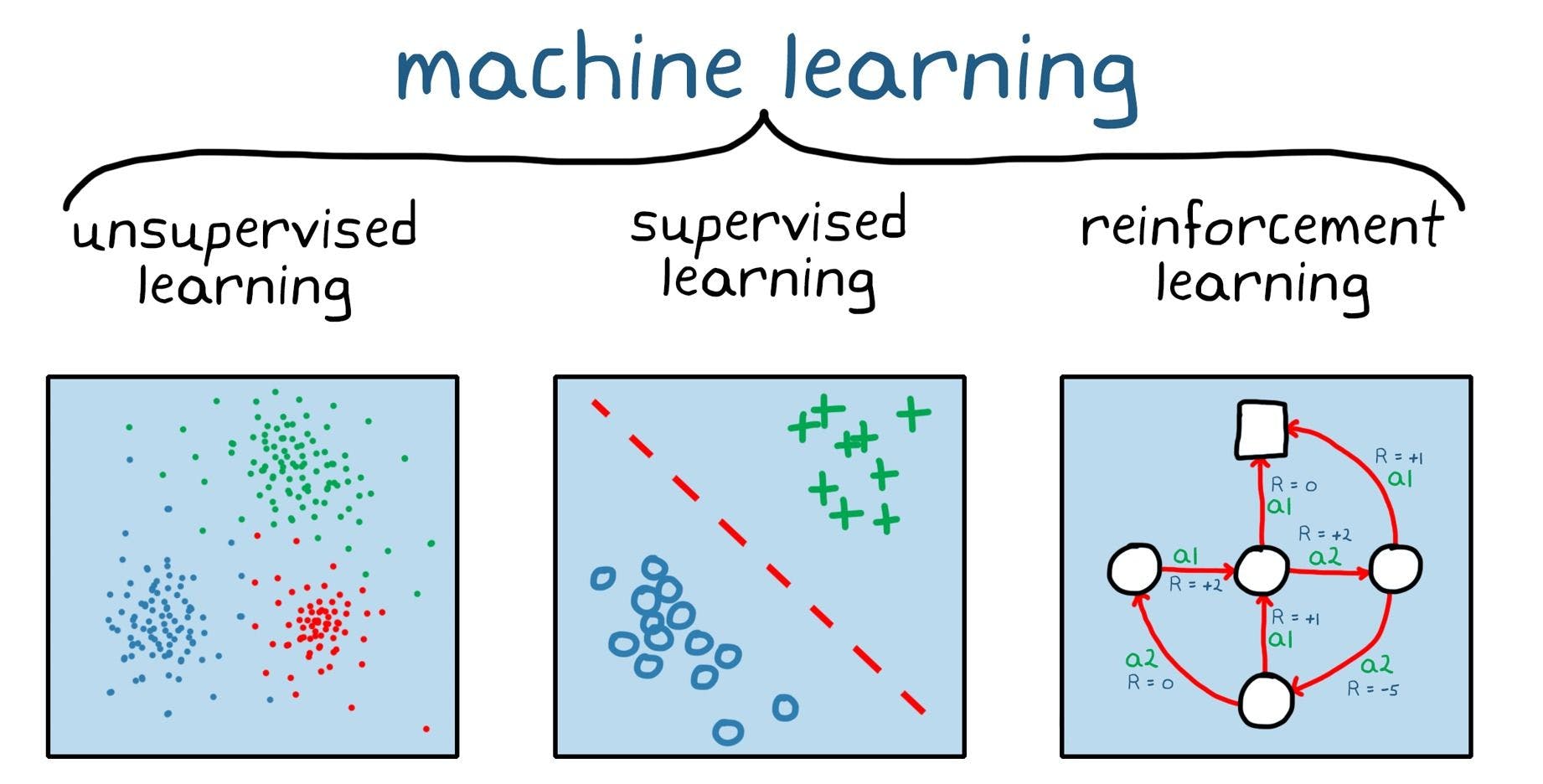
Image source: What is reinforcement learning? | MathWorks

The term ‘machine learning’ was first coined by Arthur Samuel in 1959. As data generation has increased by leaps and bounds in the past few decades, this technology has found applications in many major fields. Since making sense out of quintillion amounts of data is pretty much outside the scope of the human mind, artificial learning has stepped in to assist this decision-making process.

How an ML algorithm works

A machine learning algorithm can be roughly divided into three parts or processes:

1. A decision process: Generally, machine learning algorithms are used to predict or classify a given problem. Thus, different techniques and calculations are applied on the available data to estimate a solution.

2. An error function: This is a mathematical equation to compare and evaluate the predictions of models. Comparison is generally done when known examples are available.

3. An updating or optimization process: The algorithm shifts and optimizes its weights and biases to fit better with the data points. This process repeats until the desired accuracy for the problem is reached.

Types of Machine Learning problems

Machine learning is a versatile tool with new applications coming up now and then. These use cases are broadly divided into three categories based on the output expected:

1. Regression: Problems where generally supervised algorithms are used to find relations between several independent variables in order to predict a continuous dependent variable.

2. Classification: Uses supervised algorithms to divide the data points into two or more classes depending on the similarities of the independent variables.

3. Clustering: It is the same as classification, but the user is uncertain how many classes the data points can be divided into. Thus, this predominantly makes use of an unsupervised type learning algorithm.

Similarities and differences

Mathematical optimization and machine learning are both highly sophisticated technologies with advanced mathematics as their backbone. They require substantial amounts of data and computing power. Both are very profitable as investments by businesses as they can help drive important decisions. They make and will continue to make significant impacts in decision-making, especially as data generation advances.

Indeed, after looking at these points, the two technologies appear more similar than different but a deeper examination will throw up some significant contrasts.

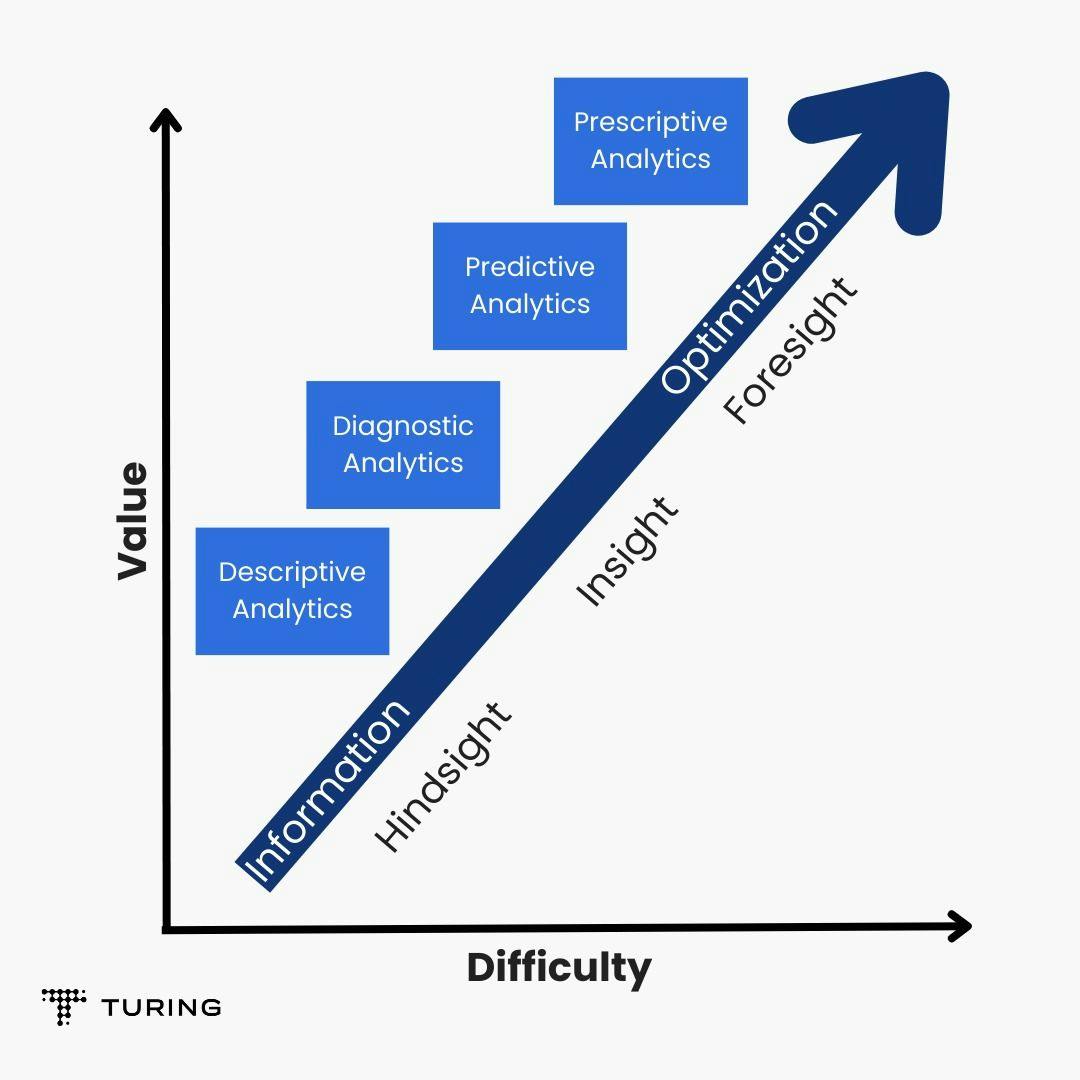
As shown, there are four types of analytics. Machine learning is predominantly a predictive analysis tool that uses a vast amount of historical data to find patterns and make predictions for the future. It helps businesses formulate long-term plans that can be beneficial for their bottom line. On the other hand, mathematical optimization is a prescriptive analysis tool. It uses the latest data to efficiently generate solutions based on optimal mathematical models and algorithms in order to make day-to-day decisions precisely and rapidly.

As mentioned earlier, the two technologies have many applications in various fields. Currently, though, machine learning seems to have endless possibilities, if there is correct data. The technologies people use across the world also leverage machine learning so that they improve with time. The technologies include speech recognition, virtual assistants, recommendation systems, spam detection, etc. Meanwhile, mathematical optimization helps businesses make decisions like employee scheduling, goods shipment, electricity distribution, etc.

Both technologies are versatile tools and are still being worked upon and perfected every day by numerous people around the world. Organizations and businesses are always ready to pay top dollar to make sounder decisions and with the latest trends in tech, these technologies will be used for years to come.