An Overview of Bayesian Networks in AI

Developing probabilistic models is challenging in AI due to the lack of information about the relationship or the dependence between random variables. Even if it is present, calculating the conditional probability of such an event can be illogical. In this scenario, developers take a common approach where they make assumptions, such as that all random variables in the model are conditionally independent. This forms the basis of Bayesian networks in artificial intelligence, which are types of probabilistic models that involve random variables that are conditionally independent.

In this blog, we will examine the working of Bayesian networks in AI with an example and explore its applications.

Understanding Bayesian networks in AI

A Bayesian network is a type of graphical model that uses probability to determine the occurrence of an event. It is also known as a belief network or a causal network. It consists of directed cyclic graphs (DCGs) and a table of conditional probabilities to find out the probability of an event happening. It contains nodes and edges, where edges connect the nodes. The graph is acyclic - meaning there is no direct path where one node can reach another. The table of probability, on the other hand, shows the likelihood that a random variable will take on certain values.

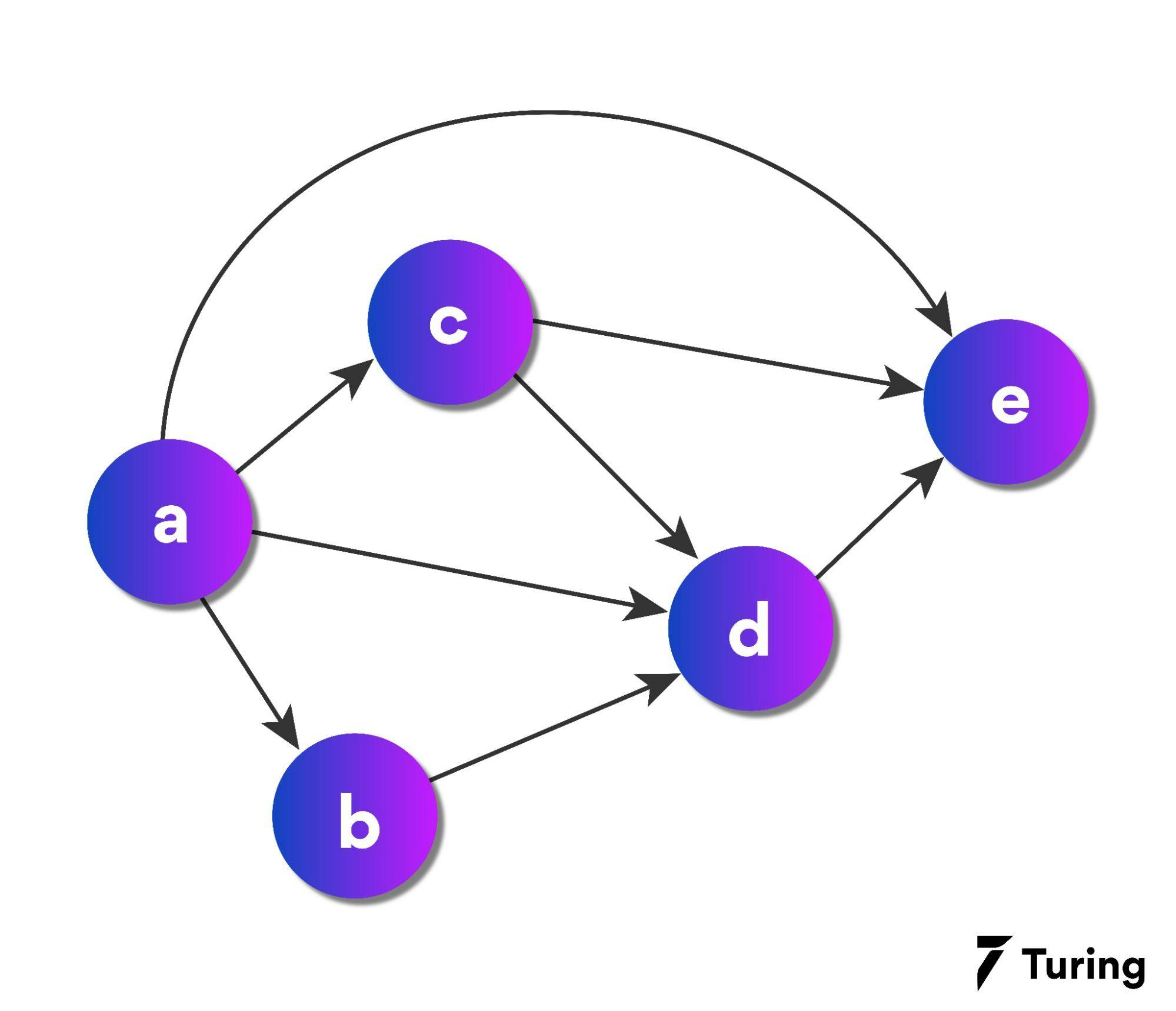
The above image illustrates a directed acyclic graph. There are five nodes, namely, a, b, c, d, and e. From the above graph, we can get the following information:

1. Node a is the parent of node b, c, and e, and node b, c, and e are the child nodes of node a.
2. Node b and c are the parent nodes of d.
3. Node e is the child node of nodes d, c, and a.

It is important to note the relationships between the nodes. Bayesian networks fall under probabilistic graphical techniques; hence, probability plays a crucial role in defining the relationship among these nodes.

There are two types of probabilities that you need to be fully aware of in Bayesian networks:

1. Joint probability

Joint probability is a probability of two or more events happening together. For example, the joint probability of two events A and B is the probability that both events occur, P(A∩B).

2. Conditional probability

Conditional probability defines the probability that event B will occur, given that event A has already occurred. There are two ways joint probability can be represented:

The conditional probability distribution of each node is represented by a table called the "node table". It contains two columns, one for each possible state of the parent node (or "parent random variable") and one for each possible state of the child node (or "child random variable").

The rows in this table correspond to all possible combinations of parent and child states. In order to find out how likely it is that a certain event will happen, we need to sum up the probabilities from all paths of that event.

Bayesian network in artificial intelligence examples

Here’s an example to better understand the concept.

You have installed a burglar alarm at home. The alarm not only detects burglary but also responds to minor earthquakes. You have two neighbors, Chris and Martin, who have agreed to get in touch with you when the alarm rings. Chris calls you when he hears the alarm but sometimes confuses it with the telephone ringing and calls. On the other hand, Martin is a music lover who sometimes misses the alarm due to the loud music he plays.

Problem:

Based on the evidence on who will or will not call, find the probability of a burglary occurring in the house.

In a Bayesian network, we can see nodes as random variables.

There are five nodes:

1. Burglary (B)
2. Earthquake (E)
3. Alarm (A)
4. Chris calls ( C )
5. Martin calls (M)

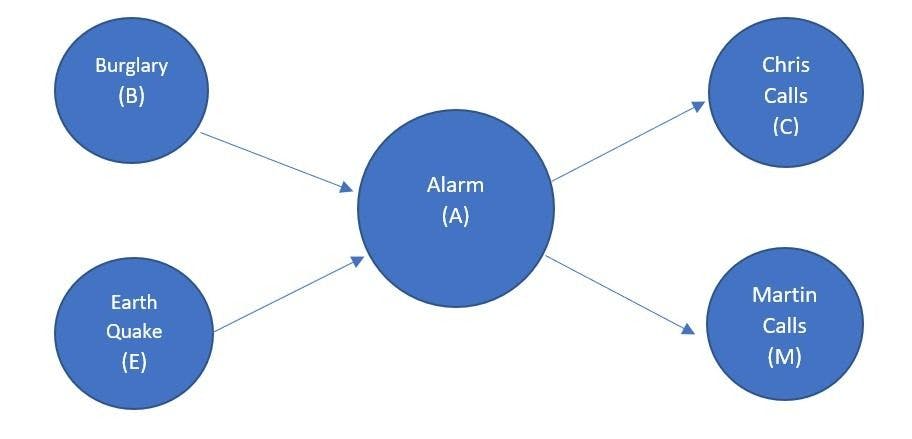
Links act as causal dependencies that define the relationship between the nodes. Both Chris and Martin call when there is an alarm.

Let’s write the probability distribution function formula for the above five nodes.

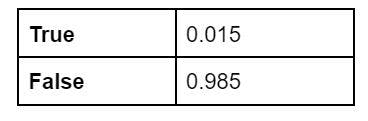
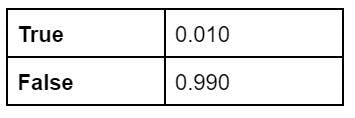
Now, let's look at the observed values for each of the nodes with the table of probabilities:

Node B:

Node E:

Node A:

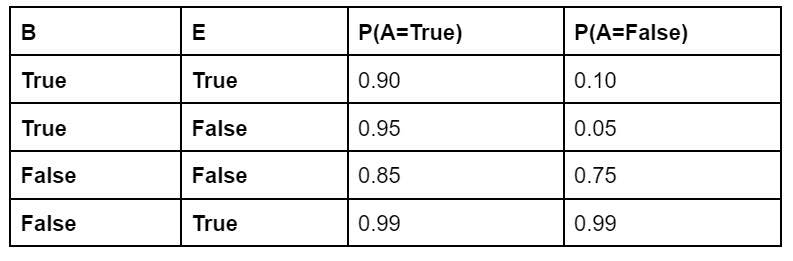
Node C:

Node M:

Based on the above observed values, the conditional values can be derived and, therefore, the probability distribution can be calculated.

Conditional values for the above nodes are:

Node A:

Node C:

Node M:

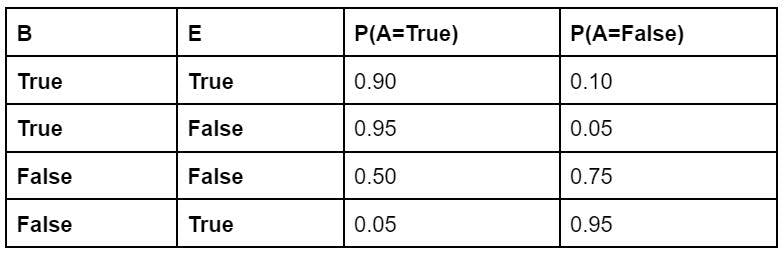
To calculate the joint distribution, we use the formula:

“P[B,E,A,C,M] = P[C | A] P[M | A] P[A | B, E] P[B | E] P[E]”

Applications of Bayesian networks in AI

Bayesian networks find applications in a variety of tasks such as:

1. Spam filtering: A spam filter is a program that helps in detecting unsolicited and spam mails. Bayesian spam filters check whether a mail is spam or not. They use filtering to learn from spam and ham messages.

2. Biomonitoring: This involves the use of indicators to quantify the concentration of chemicals in the human body. Blood or urine is used to measure the same.

3. Information retrieval: Bayesian networks assist in information retrieval for research, which is a constant process of extracting information from databases. It works in a loop. Hence, we have to continuously reconsider and redefine our research problem to avoid data overload.

4. Image processing: A form of signal processing, image processing uses mathematical operations to convert images into digital format. Once images are converted, their quality can be enhanced with more operations. The input image doesn’t necessarily have to be in the form of an image; it could be a photograph or a video frame.

5. Gene regulatory network: A Bayesian network is an algorithm that can be applied to gene regulatory networks in order to make predictions about the effects of genetic variations on cellular phenotypes. Gene regulatory networks are a set of mathematical equations that describe the interactions between genes, proteins, and metabolites. They are used to study how genetic variations affect the development of a cell or organism.

6. Turbo code: Turbo codes are a type of error correction code capable of achieving very high data rates and long distances between error correcting nodes in a communications system. They have been used in satellites, space probes, deep-space missions, military communications systems, and civilian wireless communication systems, including WiFi and 4G LTE cellular telephone systems.

7. Document classification: This is a problem often encountered in computer science and information science. Here, the main issue is to assign a document multiple classes. The task can be achieved manually and algorithmically. Since manual effort takes too much time, algorithmic documentation is done to complete it quickly and effectively.

We have seen what Bayesian networks in machine learning are and how they work. To recap, they are a type of probabilistic graphical model. The first stage of belief networks is to convert all possible states of the world into beliefs, which are either true or false. In the second stage, all possible transitions between states are encoded as conditional probabilities. The final stage is to encode all possible observations as likelihoods for each state.

A belief network can be seen as an inference procedure for a set of random variables, conditioned on some other random variables. The conditional independence assumptions define the joint probability distribution from which the conditional probabilities are computed.

FAQs

Why are Bayesian networks important in AI?

Ans: Bayesian networks are helpful for solving probabilistic problems. Such issues depend on too many variables. Since Bayesian networks are probabilistic in nature, they help predict events and derive relationships between multiple variables or events. These relationships are derived on the basis of joint and conditional probabilities.

What is the difference between Markov networks and Bayesian networks?

Ans: While both networks comprise nodes and edges, they are very different in their functioning. A Markov network is undirected and could be acyclic, while a Bayesian network is directed and acyclic.

What do Bayesian networks predict?

Ans: The sole purpose of using Bayesian networks to make probabilistic models in artificial intelligence. Such models involve many variables that are dependent on each other. Due to this, finding the probability of an event becomes difficult. Bayesian networks make the task easier as they help find the joint and conditional probability between two events effectively.

Why are Bayesian networks acyclic?

Ans: Bayesian networks need to be acyclic in order to make sure that their underlying probability distribution is normalized to 1.